-
Главная
-
Полезные советы
-
Вектор скорости точки в кинематике.
Вектор скорости точки в кинематике.
Проведем из произвольной точки О на оси вращения в точку М радиус-вектор
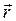
(рис. 2.7). Также изобразим в точке О векторы
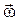
и
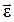
.
Рассмотрим вектор 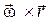 . Вычислив модуль этого вектора
. Вычислив модуль этого вектора 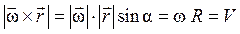 ,
,
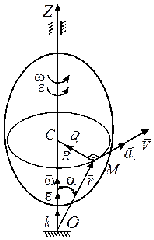 Рис. 2.7 Рис. 2.7 |
заметим, что он равен численному значению скорости точки М. Направления векторов
![clip_image008[1] clip_image008[1]](https://moscow-stud.com/wp-content/uploads/f8e102755f92_A91F/clip_image0081_thumb.gif)
и
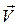
также совпадают (оба вектора направлены перпендикулярно плоскости треугольника ОМС, т. е. по касательной к окружности в направлении вращения тела).
Следовательно,

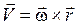
. (2.18)
Вектор скорости точки вращающегося тела равен векторному произведению угловой скорости тела на радиус-вектор точки. Формула (2.18) называется формулой Эйлера.
Согласно (1.2),
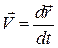
, и при вращательном движении тела радиус-вектор
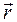
точки, изменяя своё направление, остаётся постоянным по модулю
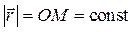
. Тогда из (2.18) получим выражение для полной производной по времени от вектора
![clip_image022[1] clip_image022[1]](https://moscow-stud.com/wp-content/uploads/f8e102755f92_A91F/clip_image0221_thumb.gif)
изменяющегося по направлению с угловой скоростью w, но постоянного по модулю:
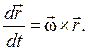
(2.19)
Для определения ускорения точки М продифференцируем по времени равенство (2.18):
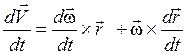
.
Отсюда находим выражение полного ускорения точки вращающегося тела
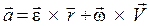
, (2.20)
где касательное и нормальное ускорения соответственно равны
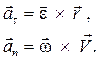
(2.21)
Действительно, модули этих векторов одинаковы:
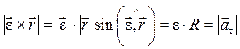
;
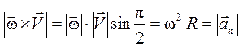
.
Вектор
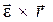
направлен так же, как вектор
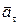
, по касательной к траектории точки М, а вектор
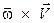
так же, как вектор нормального ускорения
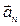
, по радиусу МС к оси вращения (см. рис 2.7).
Если испытываете трудности в написании
контрольной работы по теоретической механике, оформите заявку и Вы узнаете сроки и стоимость работы.
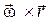 . Вычислив модуль этого вектора
. Вычислив модуль этого вектора 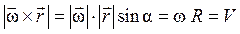 ,
,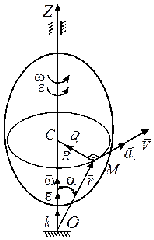 Рис. 2.7
Рис. 2.7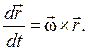 (2.19)
Для определения ускорения точки М продифференцируем по времени равенство (2.18):
(2.19)
Для определения ускорения точки М продифференцируем по времени равенство (2.18): 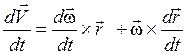 .
Отсюда находим выражение полного ускорения точки вращающегося тела
.
Отсюда находим выражение полного ускорения точки вращающегося тела 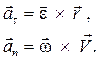 (2.21)
Действительно, модули этих векторов одинаковы:
(2.21)
Действительно, модули этих векторов одинаковы: 