1. Главная
2. Полезные советы
3. Влияние условий закрепления стержня на величину критической силы.

Влияние условий закрепления стержня на величину критической силы.

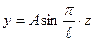
Уравнение изогнутой оси стержня при потере устойчивости определится формулой ., т.е. она представляет собой дугу синусоиды. Для рассмотренного стержня, шарнирно закрепленного по концам (эйлеровский случай), изогнутая ось принимает форму полуволны синусоиды длиной ℓ. Стержень с жестким закреплением при изгибе принимает форму четверти волны синусоиды, а полая полуволна будет располагаться на длине 2ℓ. Для такого стержня критическая сила будет равна. 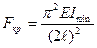Для сопоставления критической силы эйлеровского стержня с критической силой стержня, имеющего другие условия закрепления концов, вводится коэффициент приведения длины, который показывает во сколько раз следует изменить длину стержня с заданными условиями закрепления по сравнению с длиной стержня с с шарнирно закрепленными концами. Форма изогнутой оси и коэффициенты приведения её длины представлены на рисунке С учетом рассмотренного коэффициента приведения длины стержня μ критическая сила будет определяться формулой (8.3). Если испытываете трудности в написании контрольной работы по сопротивлению материалов, оформите заявку и Вы узнаете сроки и стоимость работы. Цена - от 99 рублей.