-
Главная
-
Полезные советы
-
Вычислите показатели вариации по каждой из выборок X, Y, Z: среднее арифметическое; моду; медиану.
Вычислите показатели вариации по каждой из выборок X, Y, Z: среднее арифметическое; моду; медиану.
Имеются исходные статистические данные в таблицах:
Таблица 1
Описание набора исходных данных
| № столбца |
Переменная |
Описание |
| 1 |
N |
Номер элемента выборки |
| 2 |
X |
Значения признака xi |
| 3 |
Y |
Значения признака yi |
| 4 |
Z |
Значения признака zi |
| 5 |
G |
Уровни ряда динамики gt |
Таблица 2
Файл данных
| N |
X |
Y |
Z |
G |
| 1 |
12 |
-41 |
-26 |
55 |
| 2 |
14 |
-37 |
14 |
54 |
| 3 |
8 |
-10 |
11 |
51 |
| 4 |
24 |
-72 |
-62 |
51 |
| 5 |
3 |
-10 |
-20 |
47 |
| 6 |
7 |
-19 |
-25 |
43 |
| 7 |
8 |
-20 |
38 |
43 |
| 8 |
19 |
-62 |
-51 |
42 |
| 9 |
19 |
-64 |
10 |
50 |
| 10 |
26 |
-78 |
-27 |
62 |
| 11 |
22 |
-77 |
-16 |
73 |
| 12 |
26 |
-83 |
-30 |
70 |
| 13 |
14 |
-42 |
31 |
75 |
| 14 |
26 |
-86 |
-90 |
70 |
| 15 |
5 |
-14 |
-23 |
69 |
| 16 |
13 |
-28 |
-46 |
61 |
| 17 |
8 |
-36 |
-88 |
57 |
| 18 |
27 |
-75 |
-86 |
55 |
| 19 |
12 |
-36 |
-40 |
49 |
| 20 |
12 |
-31 |
-64 |
63 |
| 21 |
25 |
-76 |
-48 |
62 |
| 22 |
17 |
-56 |
-10 |
73 |
| 23 |
12 |
-40 |
25 |
76 |
| 24 |
28 |
-78 |
-76 |
88 |
| 25 |
7 |
-13 |
-14 |
88 |
| 26 |
3 |
-14 |
-55 |
87 |
| 27 |
5 |
-11 |
-14 |
82 |
| 28 |
16 |
-56 |
-55 |
77 |
| 29 |
23 |
-72 |
-34 |
75 |
| 30 |
26 |
-82 |
-31 |
71 |
Вычислите показатели вариации по каждой из выборок X, Y, Z:
• среднее арифметическое;
• моду;
• медиану;
• размах вариации;
• дисперсию;
• стандартное отклонение;
• среднее линейное отклонение;
• коэффициенты осцилляции и вариации.
Решение:
1. Вычисление показателей вариации по выборке X.
Среднее арифметическое равно
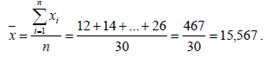
Мода – значение признака, встречающееся чаще всего. Для нахождения моды расположим все исходные данные в порядке возрастания (табл. 3).
Повторяющиеся значения записывают столько раз (ni), сколько они попадаются в исходном массиве.
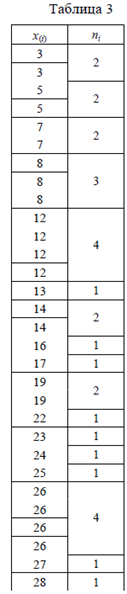
Выбираем значение с максимальной частотой:
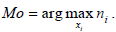
Таким образом, выборка X является двумодальной. Моды равны 12 и 26. Медиана – центральное значение вариационного ряда (табл. 4).
Таблица 4
Вариационный ряд
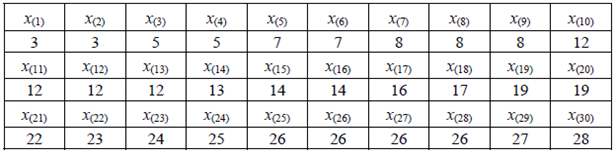
Т.к. объем выборки ( n = 30 ) четный, берем среднее арифметическое двух центральных значений
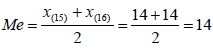
Размах вариации равен
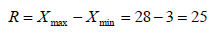
Дисперсия равна

Стандартное отклонение равно
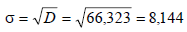
Среднее линейное отклонение:
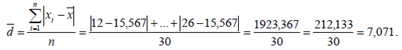
Коэффициент осцилляции равен
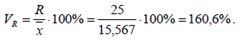
Коэффициент вариации:
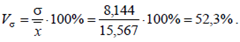
2. Вычисление показателей вариации по выборке Y.
Среднее арифметическое равно
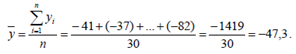
Мода – значение признака, встречающееся чаще всего. Для нахождения моды расположим все исходные данные в порядке возрастания (табл. 5).
Повторяющиеся значения записывают столько раз (ni), сколько они попадаются в исходном массиве.

Выбираем значение с максимальной частотой:
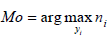
Таким образом, выборка Y является многомодальной. Моды равны -78, -72, -56, -36, -14
и -10.
Медиана – центральное значение вариационного ряда (табл. 6).
Таблица 6
Вариационный ряд
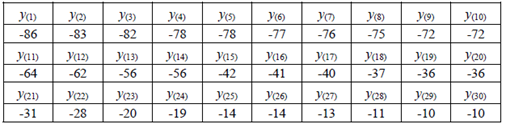
Т.к. объем выборки ( n = 30 ) четный, берем среднее арифметическое двух центральных значений
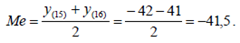
Размах вариации равен
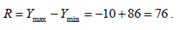
Дисперсия равна
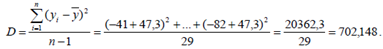
Стандартное отклонение равно
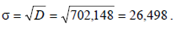
Среднее линейное отклонение:
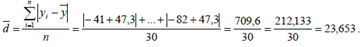
Коэффициент осцилляции равен
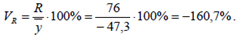
Коэффициент вариации:
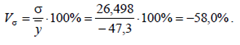
3. Вычисление показателей вариации по выборке Z.
Среднее арифметическое равно
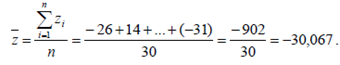
Мода – значение признака, встречающееся чаще всего. Для нахождения моды расположим все исходные данные в порядке возрастания (табл. 7). Повторяющиеся значения записывают столько раз (ni), сколько они попадаются в исходном массиве.
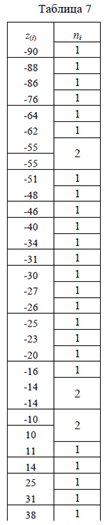
Выбираем значение с максимальной частотой:
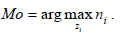
Таким образом, выборка Z является многомодальной. Моды равны -55, -14 и -10.
Медиана – центральное значение вариационного ряда (табл. 8).
Таблица 8
Вариационный ряд
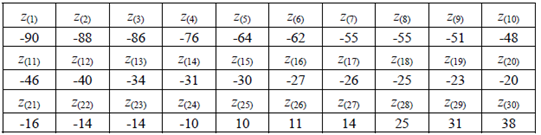
Т.к. объем выборки ( n = 30 ) четный, берем среднее арифметическое двух центральных значений
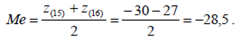
Размах вариации равен
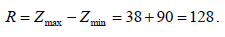
Дисперсия равна
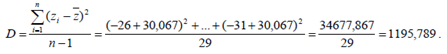
Стандартное отклонение равно
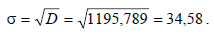
Среднее линейное отклонение:
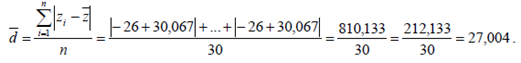
Коэффициент осцилляции равен
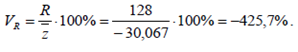
Коэффициент вариации:
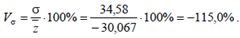
Если испытываете трудности в написании
контрольной работы по статистике, оформите заявку и Вы узнаете сроки и стоимость работы. Цена - от 99 рублей.
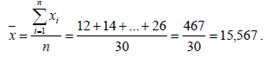 Мода – значение признака, встречающееся чаще всего. Для нахождения моды расположим все исходные данные в порядке возрастания (табл. 3).
Повторяющиеся значения записывают столько раз (ni), сколько они попадаются в исходном массиве.
Мода – значение признака, встречающееся чаще всего. Для нахождения моды расположим все исходные данные в порядке возрастания (табл. 3).
Повторяющиеся значения записывают столько раз (ni), сколько они попадаются в исходном массиве.
 Выбираем значение с максимальной частотой:
Выбираем значение с максимальной частотой:  Т.к. объем выборки ( n = 30 ) четный, берем среднее арифметическое двух центральных значений
Т.к. объем выборки ( n = 30 ) четный, берем среднее арифметическое двух центральных значений
 Стандартное отклонение равно
Стандартное отклонение равно 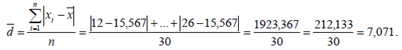 Коэффициент осцилляции равен
Коэффициент осцилляции равен 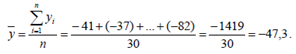 Мода – значение признака, встречающееся чаще всего. Для нахождения моды расположим все исходные данные в порядке возрастания (табл. 5).
Повторяющиеся значения записывают столько раз (ni), сколько они попадаются в исходном массиве.
Мода – значение признака, встречающееся чаще всего. Для нахождения моды расположим все исходные данные в порядке возрастания (табл. 5).
Повторяющиеся значения записывают столько раз (ni), сколько они попадаются в исходном массиве.
 Выбираем значение с максимальной частотой:
Выбираем значение с максимальной частотой:  Т.к. объем выборки ( n = 30 ) четный, берем среднее арифметическое двух центральных значений
Т.к. объем выборки ( n = 30 ) четный, берем среднее арифметическое двух центральных значений 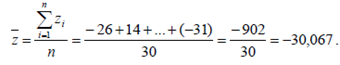 Мода – значение признака, встречающееся чаще всего. Для нахождения моды расположим все исходные данные в порядке возрастания (табл. 7). Повторяющиеся значения записывают столько раз (ni), сколько они попадаются в исходном массиве.
Мода – значение признака, встречающееся чаще всего. Для нахождения моды расположим все исходные данные в порядке возрастания (табл. 7). Повторяющиеся значения записывают столько раз (ni), сколько они попадаются в исходном массиве.
 Выбираем значение с максимальной частотой:
Выбираем значение с максимальной частотой:  Т.к. объем выборки ( n = 30 ) четный, берем среднее арифметическое двух центральных значений
Т.к. объем выборки ( n = 30 ) четный, берем среднее арифметическое двух центральных значений
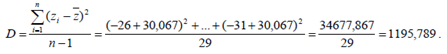 Стандартное отклонение равно
Стандартное отклонение равно 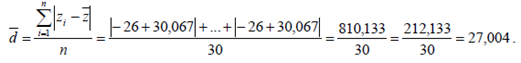 Коэффициент осцилляции равен
Коэффициент осцилляции равен 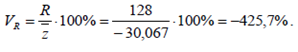 Коэффициент вариации:
Коэффициент вариации: 