-
Главная
-
Полезные советы
-
Решение задач на равновесие сил.
Решение задач на равновесие сил.
Для решения задач статики можно воспользоваться следующим планом:
1. Выбрать объект, равновесие которого следует рассмотреть. Таким объектом может быть точка, тело либо система тел.
2. Приложить действующие на этот объект силы.
3. Отбросить связи, заменив их действие реакциями .
4. Определить тип полученной системы сил. Убедиться, что число неизвестных в задаче равно числу уравнений равновесия, то есть выяснить статическую определимость задачи.
5. Выбрать оси координат. При выборе осей следует помнить, что уравнение будет проще, если в него входит меньшее количество неизвестных, то есть необходимо, по возможности, оси координат брать перпендикулярно одной из неизвестных реакций.
6. Составить уравнения равновесия, соответствующие данному виду системы сил, и решить их относительно неизвестных.
Пример (рис.1.17)
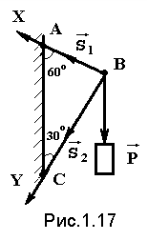
Два стержня связаны между собой и со стеной шарнирами. К шарниру В на нити подвешен груз весом 100 Н. Определить усилия в стержнях.
Решение. Поскольку стержни соединены в точке В, она будет служить объектом равновесия. Hа нее будет действовать сила натяжения нити, равная весу груза Р.
Связями для точки В служат стержни АВ и ВС. Отбрасывая связи заменим их реакциями -
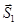
и
![clip_image002[1] clip_image002[1]](https://moscow-stud.com/wp-content/uploads/dfa68085c9e8_D251/clip_image0021_thumb.png)
, которые направлены вдоль стержня. Направляя усилия в от точки В предполагаем, что оба стержня растянуты. На точку В действуют три силы, лежащие в одной плоскости и пересекающиеся в одной точке, то есть плоская сходящаяся система сил, для которой можно составить два уравнения равновесия:
SF
кx=0 , SF
кy=0.
В этих уравнениях находится 2 неизвестных - усилия S
1 и S
2. Оси координат направим вдоль стержней. Составляем уравнения равновесия.
SF
kx=S
1-P×cos(60°)=0;
SF
ky=S
2+P×cos(30°)=0.
Из первого уравнения находим: S
1=P× cos(60°)=100×0,5=50 H,
из второго: S
2= - P×cos(30°)= - 100×0,867= - 86,7 H.
Усилие S
2 получилось отрицательным, то есть стержень ВС будет не растягиваться, а сжиматься.
![clip_image001[5] clip_image001[5]](https://moscow-stud.com/wp-content/uploads/dfa68085c9e8_D251/clip_image0015_thumb.png)
В данном решении использовался аналитический метод. Для примера приведем геометрическое решение задачи. Для этого нужно построить из сил, действующих на точку В векторный треугольник. Вначале в масштабе построим силу Р (рис.1.18). Из начала и конца этой силы проводим прямые, параллельные усилиям
![clip_image002[7] clip_image002[7]](https://moscow-stud.com/wp-content/uploads/dfa68085c9e8_D251/clip_image0027_thumb.png)
и
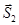
, получая, таким образом, замкнутый силовой треугольник. При этом для замыкания треугольника мы были вынуждены сменить направление усилия
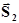
. Из треугольника, в котором усилие Р является гипотенузой, а S
1 и S
2 - катетами, находим:
S
1=P×cos(60°)=50 H,
S
2=P×cos(30°)=86,7 H.
Если испытываете трудности в написании
курсовой работы по теоретической механике, оформите заявку и Вы узнаете сроки и стоимость работы. Цена – от 99 рублей.
 Два стержня связаны между собой и со стеной шарнирами. К шарниру В на нити подвешен груз весом 100 Н. Определить усилия в стержнях.
Решение. Поскольку стержни соединены в точке В, она будет служить объектом равновесия. Hа нее будет действовать сила натяжения нити, равная весу груза Р.
Связями для точки В служат стержни АВ и ВС. Отбрасывая связи заменим их реакциями -
Два стержня связаны между собой и со стеной шарнирами. К шарниру В на нити подвешен груз весом 100 Н. Определить усилия в стержнях.
Решение. Поскольку стержни соединены в точке В, она будет служить объектом равновесия. Hа нее будет действовать сила натяжения нити, равная весу груза Р.
Связями для точки В служат стержни АВ и ВС. Отбрасывая связи заменим их реакциями -![clip_image001[5] clip_image001[5]](https://moscow-stud.com/wp-content/uploads/dfa68085c9e8_D251/clip_image0015_thumb.png) В данном решении использовался аналитический метод. Для примера приведем геометрическое решение задачи. Для этого нужно построить из сил, действующих на точку В векторный треугольник. Вначале в масштабе построим силу Р (рис.1.18). Из начала и конца этой силы проводим прямые, параллельные усилиям
В данном решении использовался аналитический метод. Для примера приведем геометрическое решение задачи. Для этого нужно построить из сил, действующих на точку В векторный треугольник. Вначале в масштабе построим силу Р (рис.1.18). Из начала и конца этой силы проводим прямые, параллельные усилиям
